–£–ī–ł–≤–ł—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —Ą–į–ļ—ā—č
–°–Ī–ĺ—Ä–Ĺ–ł–ļ —Ā–į–ľ—č—Ö –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ĺ—č—Ö —Ą–į–ļ—ā–ĺ–≤, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ľ–ĺ–≥—É—ā –≤–į—Ā —É–ī–ł–≤–ł—ā—Ć!
–§–į–ļ—ā—č –ĺ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł
–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ–ī–Ĺ–ł–ľ –ł–∑ –≤–į–∂–Ĺ–Ķ–Ļ—ą–ł—Ö —Ä–į–∑–ī–Ķ–Ľ–ĺ–≤ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ł. –ě–Ĺ–į –Ĺ–į–≥–Ľ—Ź–ī–Ĺ–ĺ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā –ĺ—ā–ĺ–Ī—Ä–į–∑–ł—ā—Ć —Ä–į–∑–Ĺ—č–Ķ –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł –ł –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ –ĺ–Ī—ä–Ķ–ļ—ā—č. –ē–Ķ –≤–ĺ–∑–Ĺ–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ł–Ķ —ć—ā–ĺ–Ļ –Ĺ–į—É–ļ–ł —É—Ö–ĺ–ī–ł—ā –≤–≥–Ľ—É–Ī—Ć –≤–Ķ–ļ–ĺ–≤ –ł —Ā–≤—Ź–∑–į–Ĺ–ĺ —Ā —Ä–į–∑–≤–ł—ā–ł–Ķ–ľ —Ä–Ķ–ľ–Ķ—Ā–Ľ–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –ī–Ķ–Ľ–į, –ļ—É–Ľ—Ć—ā—É—Ä—č –ł –ł—Ā–ļ—É—Ā—Ā—ā–≤–į, –į —ā–į–ļ–∂–Ķ —Ä—Ź–ī–į –Ĺ–į—Ā—É—Č–Ĺ—č—Ö –Ņ—Ä–į–ļ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –∑–į–ī–į—á (–ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–Ķ –∑–Ķ–ľ–Ķ–Ľ—Ć–Ĺ—č—Ö —É—á–į—Ā—ā–ļ–ĺ–≤ –ł –ĺ–Ī—ä–Ķ–ľ–ĺ–≤ —ā–Ķ–Ľ).
–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į –ī–Ľ—Ź –ī—Ä–Ķ–≤–Ĺ–ł—Ö –≥—Ä–Ķ–ļ–ĺ–≤ –Ī—č–Ľ–į, –Ņ—Ä–Ķ–∂–ī–Ķ –≤—Ā–Ķ–≥–ĺ, –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ. –ü–ĺ—ć—ā–ĺ–ľ—É –Ĺ–į–ī –ī–≤–Ķ—Ä–ł –ź–ļ–į–ī–Ķ–ľ–ł–ł, –≤ —Ā—ā–Ķ–Ĺ–į—Ö –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –ü–Ľ–į—ā–ĺ–Ĺ —É—á–ł–Ľ —Ā–≤–ĺ–ł—Ö —É—á–Ķ–Ĺ–ł–ļ–ĺ–≤, –≤–ł—Ā–Ķ–Ľ–į –Ĺ–į–ī–Ņ–ł—Ā—Ć: ¬ę–ü—É—Ā—ā—Ć —Ā—é–ī–į –Ĺ–Ķ –≤—Ö–ĺ–ī–ł—ā —ā–ĺ—ā, –ļ—ā–ĺ –Ĺ–Ķ –∑–Ĺ–į–Ķ—ā –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł¬Ľ.
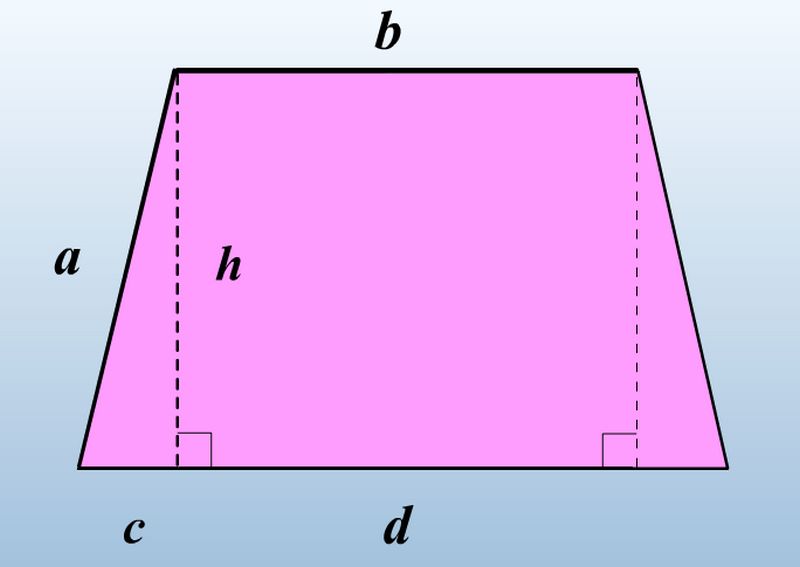 –Ę—Ä–į–Ņ–Ķ—Ü–ł—Ź - –ĺ—á–Ķ–Ĺ—Ć –ł–∑–≤–Ķ—Ā—ā–Ĺ–į—Ź –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–į—Ź —Ą–ł–≥—É—Ä–į
–Ę—Ä–į–Ņ–Ķ—Ü–ł—Ź - –ĺ—á–Ķ–Ĺ—Ć –ł–∑–≤–Ķ—Ā—ā–Ĺ–į—Ź –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–į—Ź —Ą–ł–≥—É—Ä–į–°–Ľ–ĺ–≤–ĺ ¬ę—ā—Ä–į–Ņ–Ķ—Ü–ł—Ź¬Ľ –Ņ—Ä–ĺ–ł–∑–ĺ—ą–Ľ–ĺ –ĺ—ā –ī—Ä–Ķ–≤–Ĺ–Ķ–≥—Ä–Ķ—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ā–Ľ–ĺ–≤–į ¬ę—ā—Ä–į–Ņ–Ķ–∑–ł–ĺ–ŬĽ (–ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā —Ā—ā–ĺ–Ľ–ł–ļ). —ā–į–ļ–∂–Ķ –ĺ—ā –ī–į–Ĺ–Ĺ–ĺ–≥–ĺ —Ā–Ľ–ĺ–≤–į –Ņ—Ä–ĺ–ł–∑–ĺ—ą–Ľ–ł —É–∂–Ķ –Ĺ–Ķ–ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ–ī–∑–į–Ī—č—ā—č–Ķ –≤ –ĺ–Ī–ł—Ö–ĺ–ī–Ķ —Ā–Ľ–ĺ–≤–į, —ā–į–ļ–ł–Ķ –ļ–į–ļ ¬ę—ā—Ä–į–Ņ–Ķ–∑–į¬Ľ –ł –Ņ—Ä–ĺ—á–ł–Ķ —Ä–ĺ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ –Ķ–ľ—É —Ā–Ľ–ĺ–≤–į.
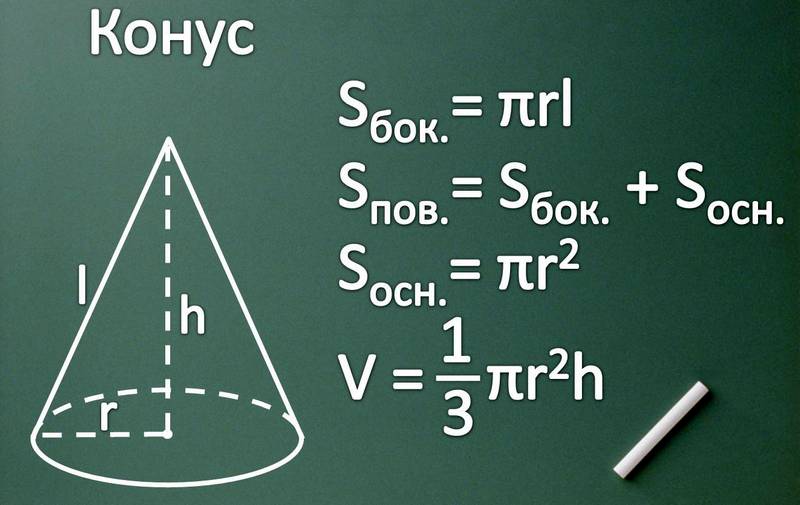 –†–ł—Ā—É–Ĺ–ĺ–ļ –ł —Ą–ĺ—Ä–ľ—É–Ľ—č –ļ–ĺ–Ĺ—É—Ā–į
–†–ł—Ā—É–Ĺ–ĺ–ļ –ł —Ą–ĺ—Ä–ľ—É–Ľ—č –ļ–ĺ–Ĺ—É—Ā–į–ď—Ä–Ķ—á–Ķ—Ā–ļ–ĺ–Ķ —Ā–Ľ–ĺ–≤–ĺ ¬ę–ļ–ĺ–Ĺ–ĺ—Ā¬Ľ, –ĺ–Ī–ĺ–∑–Ĺ–į—á–į—é—Č–Ķ–Ķ —Ā–ĺ—Ā–Ĺ–ĺ–≤—É—é —ą–ł—ą–ļ—É, —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ā–Ľ–ĺ–≤–į—Ä–Ĺ–ĺ–Ļ –ĺ—Ā–Ĺ–ĺ–≤–ĺ–Ļ –ī–Ľ—Ź —ā–į–ļ–ĺ–≥–ĺ —ā–Ķ—Ä–ľ–ł–Ĺ–į –ļ–į–ļ ¬ę–ļ–ĺ–Ĺ—É—Ā¬Ľ, –į –ł–∑–≤–Ķ—Ā—ā–Ĺ—č–Ļ –≤ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł —ā–Ķ—Ä–ľ–ł–Ĺ ¬ę–Ľ–ł–Ĺ–ł—Ź¬Ľ –≤–ĺ–∑–Ĺ–ł–ļ —É–∂–Ķ –ĺ—ā –Ľ–į—ā–ł–Ĺ—Ā–ļ–ĺ–≥–ĺ —Ā–Ľ–ĺ–≤–į ¬ę–Ľ–ł–Ĺ—É–ľ¬Ľ (—á—ā–ĺ –≤ –Ņ–Ķ—Ä–Ķ–≤–ĺ–ī–Ķ –Ĺ–į —Ä—É—Ā—Ā–ļ–ł–Ļ —Ź–∑—č–ļ –ĺ–∑–Ĺ–į—á–į–Ķ—ā ¬ę–Ľ—Ć–Ĺ—Ź–Ĺ–į—Ź –Ĺ–ł—ā—ƬĽ).
 –ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą–ł–≥—É—Ä—č
–ď–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą–ł–≥—É—Ä—č–°—Ä–Ķ–ī–ł –≤—Ā–Ķ—Ö –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą–ĺ—Ä–ľ —Ā –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤—č–ľ –Ņ–Ķ—Ä–ł–ľ–Ķ—ā—Ä–ĺ–ľ, –ļ—Ä—É–≥ –ł–ľ–Ķ–Ķ—ā –Ĺ–į–ł–Ī–ĺ–Ľ—Ć—ą—É—é –Ņ–Ľ–ĺ—Č–į–ī—Ć –ł, –Ĺ–į–ĺ–Ī–ĺ—Ä–ĺ—ā, —Ā—Ä–Ķ–ī–ł –≤—Ā–Ķ—Ö —Ą–ł–≥—É—Ä —Ā –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤–ĺ–Ļ –Ņ–Ľ–ĺ—Č–į–ī—Ć—é –ļ—Ä—É–≥ –ł–ľ–Ķ–Ķ—ā –Ĺ–į–ł–ľ–Ķ–Ĺ—Ć—ą–ł–Ļ –Ņ–Ķ—Ä–ł–ľ–Ķ—ā—Ä. ¬ę–ö–≤–į–ī—Ä–į—ā—É—Ä–į –ļ—Ä—É–≥–į¬Ľ - —ć—ā–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į—Ź –∑–į–ī–į—á–į, –ļ–ĺ—ā–ĺ—Ä–į—Ź –∑–į–ļ–Ľ—é—á–į–Ķ—ā—Ā—Ź –≤ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–ľ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–ł –Ņ—Ä–ł –Ņ–ĺ–ľ–ĺ—Č–ł —Ü–ł—Ä–ļ—É–Ľ—Ź –ł –Ľ–ł–Ĺ–Ķ–Ļ–ļ–ł, –ļ–≤–į–ī—Ä–į—ā–į, —Ä–į–≤–Ĺ–ĺ–≤–Ķ–Ľ–ł–ļ–ĺ–≥–ĺ –Ņ–ĺ –Ņ–Ľ–ĺ—Č–į–ī–ł –ī–į–Ĺ–Ĺ–ĺ–ľ—É –ļ—Ä—É–≥—É. –í 1882 –≥–ĺ–ī—É, –§–Ķ—Ä–ī–ł–Ĺ–į–Ĺ–ī–ĺ–ľ –õ–ł–Ĺ–ī–Ķ–ľ–į–Ĺ–ĺ–ľ, –Ī—č–Ľ–į –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ī–ĺ–ļ–į–∑–į–Ĺ–į –Ĺ–Ķ—Ä–į–∑—Ä–Ķ—ą–ł–ľ–ĺ—Ā—ā—Ć —ć—ā–ĺ–Ļ –∑–į–ī–į—á–ł. –ĺ–ī–Ĺ–į–ļ–ĺ —ć—ā–ĺ, –Ĺ–Ķ –Ņ–ĺ–ľ–Ķ—ą–į–Ľ–ĺ –ľ–Ĺ–ĺ–≥–ł–ľ –Ľ—é–ī—Ź–ľ –Ņ—Ä–ĺ–ī–ĺ–Ľ–∂–ł—ā—Ć —ā—Ä–į—ā–ł—ā—Ć —Ā–≤–ĺ—Ď –≤—Ä–Ķ–ľ—Ź –Ĺ–į –Ķ—Ď —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ. –Ę–į–ļ –Ņ–ĺ—Ź–≤–ł–Ľ–į—Ā—Ć –ł–∑–≤–Ķ—Ā—ā–Ĺ–į—Ź –≤—Ā–Ķ–ľ –ľ–Ķ—ā–į—Ą–ĺ—Ä–į –ĺ–Ī—É—Ā–Ľ–ĺ–≤–Ľ–Ķ–Ĺ–Ĺ–į—Ź –ł–ľ–Ķ–Ĺ–Ĺ–ĺ –Ī–Ķ—Ā–Ņ–Ķ—Ä—Ā–Ņ–Ķ–ļ—ā–ł–≤–Ĺ–ĺ—Ā—ā—Ć –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č—Ö –ł–∑—č—Ā–ļ–į–Ĺ–ł–Ļ.
 –ö–į–ļ —Ä–į–∑—Ä–Ķ–∑–į—ā—Ć –Ņ–ł—Ä–ĺ–≥ –Ĺ–į 8 —á–į—Ā—ā–Ķ–Ļ?
–ö–į–ļ —Ä–į–∑—Ä–Ķ–∑–į—ā—Ć –Ņ–ł—Ä–ĺ–≥ –Ĺ–į 8 —á–į—Ā—ā–Ķ–Ļ?–ü–ł—Ä–ĺ–≥ —Ä–į–∑—Ä–Ķ–∑–į–Ķ—ā—Ā—Ź –≤—Ā–Ķ–≥–ĺ —ā—Ä–Ķ–ľ—Ź –ļ–į—Ā–į–Ĺ–ł—Ź–ľ–ł –Ĺ–ĺ–∂–į –Ĺ–į –≤–ĺ—Ā–Ķ–ľ—Ć —Ä–į–≤–Ĺ—č—Ö –ī–ĺ–Ľ–Ķ–Ļ. –ü—Ä–ł—á–Ķ–ľ, —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā —ā–ĺ–Ľ—Ć–ļ–ĺ –ī–≤–į —Ā–Ņ–ĺ—Ā–ĺ–Ī–į —ć—ā–ĺ —Ā–ī–Ķ–Ľ–į—ā—Ć.
–ü–ĺ–ī —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–ľ –†—Ď–Ľ–ĺ –Ņ–ĺ–Ĺ–ł–ľ–į—é—ā –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ—É—é —Ą–ł–≥—É—Ä—É, –ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–Ĺ—É—é –Ņ–Ķ—Ä–Ķ—Ā–Ķ—á–Ķ–Ĺ–ł–Ķ–ľ 3 –ļ—Ä—É–≥–ĺ–≤ –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤–ĺ–≥–ĺ —Ä–į–ī–ł—É—Ā–į D —Ā —Ü–Ķ–Ĺ—ā—Ä–į–ľ–ł, –Ĺ–į—Ö–ĺ–ī—Ź—Č–ł–ľ–ł—Ā—Ź –≤ –≤–Ķ—Ä—ą–ł–Ĺ–į—Ö —Ä–į–≤–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į, —ā–į–ļ–ĺ–Ļ –∂–Ķ –Ņ–ĺ –ī–Ľ–ł–Ĺ–Ķ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č. –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –†—Ď–Ľ–ĺ –Ī—č–Ľ–ĺ –Ņ—Ä–ł–ī—É–ľ–į–Ĺ–ĺ —Ā–≤–Ķ—Ä–Ľ–ĺ, –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź—é—Č–Ķ–Ķ –Ņ—Ä–ĺ—Ā–≤–Ķ—Ä–Ľ–ł–≤–į—ā—Ć –Ņ–ĺ—á—ā–ł –ļ–≤–į–ī—Ä–į—ā–Ĺ—č–Ķ –ĺ—ā–≤–Ķ—Ä—Ā—ā–ł—Ź.
–§–į–ļ—ā—č –ĺ —Ą—Ä–į–ļ—ā–į–Ľ—Ć–Ĺ–ĺ–Ļ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł
–ü—Ä–į–≤–ł–Ľ–ĺ –≤—č–≤–Ķ–ī–Ķ–Ĺ–Ĺ–ĺ–Ķ –∑–Ĺ–į–ľ–Ķ–Ĺ–ł—ā—č–ľ –ł—ā–į–Ľ—Ć—Ź–Ĺ—Ā–ļ–ł–ľ —É—á—Ď–Ĺ—č–ľ –õ–Ķ–ĺ–Ĺ–į—Ä–ī–ĺ–ľ –ī–į –í–ł–Ĺ—á–ł –≥–Ľ–į—Ā–ł—ā, —á—ā–ĺ –ļ–≤–į–ī—Ä–į—ā –ī–ł–į–ľ–Ķ—ā—Ä–į (D) —Ā—ā–≤–ĺ–Ľ–į –ī–Ķ—Ä–Ķ–≤–į —Ä–į–≤–Ķ–Ĺ —Ā—É–ľ–ľ–Ķ –ļ–≤–į–ī—Ä–į—ā–ĺ–≤ –ī–ł–į–ľ–Ķ—ā—Ä–ĺ–≤ (d1 –ł d2) –≤–Ķ—ā–≤–Ķ–Ļ, –≤–∑—Ź—ā—č—Ö –Ĺ–į –ĺ–Ī—Č–Ķ–Ļ —Ą–ł–ļ—Ā–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ –≤—č—Ā–ĺ—ā–Ķ. –Ď–ĺ–Ľ–Ķ–Ķ –Ņ–ĺ–∑–ī–Ĺ–ł–Ķ –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł—Ź –Ņ–ĺ–ī—ā–≤–Ķ—Ä–ī–ł–Ľ–ł –ī–į–Ĺ–Ĺ–ĺ–Ķ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –Ľ–ł—ą—Ć —Ā –ĺ–ī–Ĺ–ĺ–Ļ –ĺ–≥–ĺ–≤–ĺ—Ä–ļ–ĺ–Ļ ‚ÄĒ —Ā—ā–Ķ–Ņ–Ķ–Ĺ—Ć –≤ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ –Ĺ–Ķ–ĺ–Ī—Ź–∑–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ī–ĺ–Ľ–∂–Ĺ–į —Ä–į–≤–Ĺ—Ź—ā—Ć—Ā—Ź –ī–≤—É–ľ, –į –ľ–ĺ–∂–Ķ—ā –Ľ–Ķ–∂–į—ā—Ć –≤ –ī–ł–į–Ņ–į–∑–ĺ–Ĺ–Ķ —á–ł—Ā–Ķ–Ľ –ĺ—ā 1,8 –ī–ĺ 2,3.
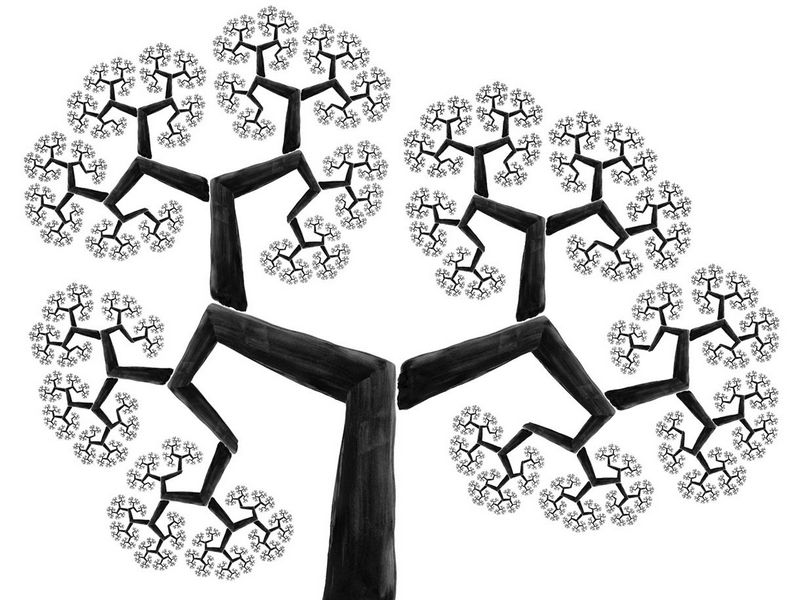 –†–ł—Ā—É–Ĺ–ĺ–ļ —Ą—Ä–į–ļ—ā–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ī–Ķ—Ä–Ķ–≤–į
–†–ł—Ā—É–Ĺ–ĺ–ļ —Ą—Ä–į–ļ—ā–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ī–Ķ—Ä–Ķ–≤–į–ü–Ķ—Ä–≤–ĺ–Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ —Ā—á–ł—ā–į–Ľ–ĺ—Ā—Ć, —á—ā–ĺ —ā–į–ļ–į—Ź –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā—Ć –ĺ–Ī—ä—Ź—Ā–Ĺ—Ź–Ķ—ā—Ā—Ź —ā–Ķ–ľ, —á—ā–ĺ –ī–Ľ—Ź –ī–Ķ—Ä–Ķ–≤–į —Ā –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ĺ–Ļ —Ā—ā—Ä—É–ļ—ā—É—Ä–ĺ–Ļ –ł–ľ–Ķ–Ķ—ā—Ā—Ź –Ī–ĺ–Ľ–Ķ–Ķ –ĺ–Ņ—ā–ł–ľ–į–Ľ—Ć–Ĺ—č–Ļ –ľ–Ķ—Ö–į–Ĺ–ł–∑–ľ —Ā–Ĺ–į–Ī–∂–Ķ–Ĺ–ł—Ź –≤–Ķ—ā–ĺ–ļ –Ņ–ł—ā–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł —Ā–ĺ–ļ–į–ľ–ł. –Ě–ĺ, –≤ 2010 –≥–ĺ–ī—É, –į–ľ–Ķ—Ä–ł–ļ–į–Ĺ—Ā–ļ–ł–ľ —Ą–ł–∑–ł–ļ–ĺ–ľ –ö—Ä–ł—Ā—ā–ĺ—Ą–ĺ–ľ –≠–Ľ–Ľ–ĺ–Ļ–Ķ–ľ –Ī—č–Ľ–ĺ –Ņ—Ä–ł–ī—É–ľ–į–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā–ĺ–Ķ –ĺ–Ī—ä—Ź—Ā–Ĺ–Ķ–Ĺ–ł–Ķ –ī–į–Ĺ–Ĺ–ĺ–ľ—É —Ą–Ķ–Ĺ–ĺ–ľ–Ķ–Ĺ—É. –ü—Ä–ł —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ–ł–ł –ī–Ķ—Ä–Ķ–≤–į –ļ–į–ļ —Ą—Ä–į–ļ—ā–į–Ľ, —É–ľ–Ķ–Ĺ—Ć—ą–į–Ķ—ā—Ā—Ź –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć —Ā–Ľ–ĺ–ľ–į –≤–Ķ—ā–ĺ–ļ –Ņ–ĺ–ī —Ā–ł–Ľ—Ć–Ĺ—č–ľ–ł –Ņ–ĺ—Ä—č–≤–į–ľ–ł –≤–Ķ—ā—Ä–į.
 –£–≥–ĺ–Ľ —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ľ–ł—Ā—ā—Ć–Ķ–≤ –ī—Ä—É–≥ –ĺ—ā –ī—Ä—É–≥–į –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –ĺ–Ņ–ł—Ā–į–Ĺ –ī—Ä–ĺ–Ī—Ć—é
–£–≥–ĺ–Ľ —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ľ–ł—Ā—ā—Ć–Ķ–≤ –ī—Ä—É–≥ –ĺ—ā –ī—Ä—É–≥–į –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –ĺ–Ņ–ł—Ā–į–Ĺ –ī—Ä–ĺ–Ī—Ć—é–õ–ł—Ā—ā—Ć—Ź –Ĺ–į –≤–Ķ—ā–≤—Ź—Ö –ī–Ķ—Ä–Ķ–≤—Ć–Ķ–≤, –ļ–į–ļ —Ā—ā–į–Ľ–ĺ –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, –≤—Ā–Ķ–≥–ī–į —Ä–į—Ā–Ņ–ĺ–Ľ–į–≥–į—é—ā—Ā—Ź –≤ —Ā—ā—Ä–ĺ–≥–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–ľ –Ņ–ĺ—Ä—Ź–ī–ļ–Ķ. –ě–Ĺ–ł –ĺ—ā—Ā—ā–ĺ—Ź—ā –ī—Ä—É–≥ –ĺ—ā –ī—Ä—É–≥–į –Ĺ–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č–Ļ —É–≥–ĺ–Ľ. –í–Ķ–Ľ–ł—á–ł–Ĺ–į —ć—ā–ĺ–≥–ĺ —É–≥–Ľ–į —Ä–į–∑–Ĺ–į—Ź –ī–Ľ—Ź —Ä–į–∑–Ĺ—č—Ö —Ä–į—Ā—ā–Ķ–Ĺ–ł–Ļ, –ĺ–ī–Ĺ–į–ļ–ĺ, —á—ā–ĺ —Ā–į–ľ–ĺ–Ķ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ĺ–ĺ–Ķ, –ĺ–Ĺ–į –≤—Ā–Ķ–≥–ī–į –ĺ–Ņ–ł—Ā—č–≤–į–Ķ—ā—Ā—Ź –Ņ—Ä–ĺ—Ā—ā–ĺ–Ļ –ī—Ä–ĺ–Ī—Ć—é, –≥–ī–Ķ —á–ł—Ā–Ľ–ł—ā–Ķ–Ľ—Ć –ł –∑–Ĺ–į–ľ–Ķ–Ĺ–į—ā–Ķ–Ľ—Ć –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ—č —á–ł—Ā–Ľ–į–ľ–ł –ł–∑ —Ä—Ź–ī–į –§–ł–Ī–ĺ–Ĺ–į—á—á–ł. –ö –Ņ—Ä–ł–ľ–Ķ—Ä—É, –Ľ–ł—Ā—ā—Ć—Ź –Ī—É–ļ–į –ĺ–Ī—Ä–į–∑—É—é—ā —É–≥–ĺ–Ľ —Ä–į–≤–Ĺ—č–Ļ 1/3, –ł–Ľ–ł 120¬į, –ī–Ľ—Ź –ī—É–Ī–į –ł –į–Ī—Ä–ł–ļ–ĺ—Ā–į –ĺ–Ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ –ī—Ä–ĺ–Ī—Ć—é 2/5, —É –≥—Ä—É—ą–ł –ł —ā–ĺ–Ņ–ĺ–Ľ—Ź ‚ÄĒ 3/8, —É –ł–≤—č –ł –ľ–ł–Ĺ–ī–į–Ľ—Ź ‚ÄĒ 5/13 –ł —ā.–ī. –ü–ĺ–ī–ĺ–Ī–Ĺ–ĺ–Ķ —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –ī–į—Ď—ā –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –Ľ–ł—Ā—ā—Ć—Ź–ľ –Ī–ĺ–Ľ–Ķ–Ķ —ć—Ą—Ą–Ķ–ļ—ā–ł–≤–Ĺ–ĺ –ł–∑–≤–Ľ–Ķ–ļ–į—ā—Ć –≤–Ľ–į–≥—É –ł –Ņ–ĺ–Ľ—É—á–į—ā—Ć —Ā–ĺ–Ľ–Ĺ–Ķ—á–Ĺ—č–Ļ —Ā–≤–Ķ—ā.
 –ö–ĺ—á–į–Ĺ –ļ–į–Ņ—É—Ā—ā—č —Ā–ĺ—Ä—ā–į –†–ĺ–ľ–į–Ĺ–Ķ—Ā–ļ–ĺ
–ö–ĺ—á–į–Ĺ –ļ–į–Ņ—É—Ā—ā—č —Ā–ĺ—Ä—ā–į –†–ĺ–ľ–į–Ĺ–Ķ—Ā–ļ–ĺ–ö—Ä–į—Ā–ł–≤–Ķ–Ļ—ą–ł–Ķ —Ā–ĺ—Ü–≤–Ķ—ā–ł—Ź –ļ–į–Ņ—É—Ā—ā—č —Ā–ĺ—Ä—ā–į —Ä–ĺ–ľ–į–Ĺ–Ķ—Ā–ļ–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā —Ā–ĺ–Ī–ĺ–Ļ —Ą—Ä–į–ļ—ā–į–Ľ—č –Ņ—Ä–ł—Ä–ĺ–ī–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ–ł—Ā—Ö–ĺ–∂–ī–Ķ–Ĺ–ł—Ź. –Ď—É—ā–ĺ–Ĺ—č —ć—ā–ĺ–≥–ĺ —Ā–ĺ—Ä—ā–į –ļ–į–Ņ—É—Ā—ā—č –ĺ–Ņ–ł—Ā—č–≤–į—é—ā—Ā—Ź —Ā—ā—Ä–ĺ–≥–ĺ–Ļ –Ľ–ĺ–≥–į—Ä–ł—Ą–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–Ņ–ł—Ä–į–Ľ—Ć—é –ł —Ā–ĺ—Ā—ā–ĺ—Ź—ā –ł–∑ –Ī–ĺ–Ľ–Ķ–Ķ –ľ–Ķ–Ľ–ļ–ł—Ö –Ī—É—ā–ĺ–Ĺ–ĺ–≤, –∑–į–ļ—Ä—É—á–Ķ–Ĺ–Ĺ—č—Ö –Ņ–ĺ —ā–ĺ–ľ—É –∂–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ—É. –Ē–į–Ĺ–Ĺ–į—Ź —Ā–į–ľ–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–į—Ź —Ā—ā—Ä—É–ļ—ā—É—Ä–į –Ņ–ĺ–≤—ā–ĺ—Ä—Ź–Ķ—ā—Ā—Ź –Ķ—Č—Ď –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ —Ä–į–∑.
 –£–∑–Ľ—č –Ĺ–į –≤–Ķ—Ä–Ķ–≤–ļ–Ķ
–£–∑–Ľ—č –Ĺ–į –≤–Ķ—Ä–Ķ–≤–ļ–Ķ–ü–ĺ—á—ā–ł 5000 –Ľ–Ķ—ā –Ĺ–į–∑–į–ī –ī—Ä–Ķ–≤–Ĺ–ł–Ķ –Ķ–≥–ł–Ņ—ā—Ź–Ĺ–Ķ —É–∂–Ķ –∑–Ĺ–į–Ľ–ł, —á—ā–ĺ –Ķ—Ā–Ľ–ł –∑–į–≤—Ź–∑–į—ā—Ć –Ĺ–į –≤–Ķ—Ä–Ķ–≤–ļ–Ķ –ī–≤–Ķ–Ĺ–į–ī—Ü–į—ā—Ć —É–∑–Ķ–Ľ–ļ–ĺ–≤ –ĺ—ā—Ā—ā–ĺ—Ź—Č–ł—Ö –ī—Ä—É–≥ –ĺ—ā –ī—Ä—É–≥–į –Ĺ–į —Ä–į–≤–Ĺ—č—Ö —Ä–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź—Ö, –į –∑–į—ā–Ķ–ľ –Ĺ–į—ā—Ź–Ĺ—É—ā—Ć –Ķ–Ķ –≤ —Ą–ĺ—Ä–ľ–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į, —ā–ĺ –ĺ–Ī—Ä–į–∑—É–Ķ—ā—Ā—Ź —Ą–ł–≥—É—Ä–į —Ā –ĺ–ī–Ĺ–ł–ľ –Ņ—Ä—Ź–ľ—č–ľ —É–≥–Ľ–ĺ–ľ. –≠—ā–ĺ –∑–Ĺ–į–Ĺ–ł–Ķ –Ņ–ĺ–ľ–ĺ–≥–į–Ľ–ĺ –ī–Ķ–Ľ–į—ā—Ć –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—É—é —Ä–į–∑–ľ–Ķ—ā–ļ—É –Ņ–Ľ–ĺ–ī–ĺ—Ä–ĺ–ī–Ĺ—č—Ö –∑–Ķ–ľ–Ķ–Ľ—Ć –≤ –ī–ĺ–Ľ–ł–Ĺ–Ķ –Ě–ł–Ľ–į.
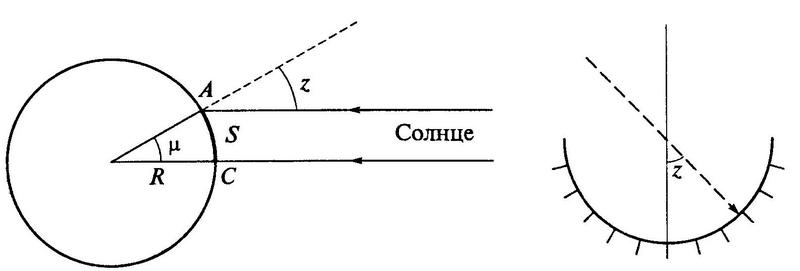 –†–ł—Ā—É–Ĺ–ĺ–ļ —Ä–į—Ā—á–Ķ—ā–į –ī–Ľ–ł–Ĺ—č –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł (–ľ–Ķ—Ä–ł–ī–ł–į–Ĺ–į) –ó–Ķ–ľ–Ľ–ł
–†–ł—Ā—É–Ĺ–ĺ–ļ —Ä–į—Ā—á–Ķ—ā–į –ī–Ľ–ł–Ĺ—č –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł (–ľ–Ķ—Ä–ł–ī–ł–į–Ĺ–į) –ó–Ķ–ľ–Ľ–ł–ü—Ä–ł –Ņ–ĺ–ľ–ĺ—Č–ł –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ł—Ö –Ņ—Ä–į–≤–ł–Ľ –ł –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ĺ —ā–ĺ–ľ, —á—ā–ĺ –Ĺ–į—ą–į –∑–Ķ–ľ–Ľ—Ź —ą–į—Ä–ĺ–ĺ–Ī—Ä–į–∑–Ĺ–į, –ī—Ä–Ķ–≤–Ĺ–Ķ–≥—Ä–Ķ—á–Ķ—Ā–ļ–ł–Ļ —É—á–Ķ–Ĺ—č–Ļ –≠—Ä–į—ā–ĺ—Ā—Ą–Ķ–Ĺ –ł–∑–ľ–Ķ—Ä–ł–Ľ –ī–Ľ–ł–Ĺ—É –Ķ—Ď –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł. –ė–ľ –Ī—č–Ľ–ĺ –∑–į–ľ–Ķ—á–Ķ–Ĺ–ĺ, —á—ā–ĺ, –ļ–ĺ–≥–ī–į –°–ĺ–Ľ–Ĺ—Ü–Ķ –Ĺ–į—Ö–ĺ–ī–ł—ā—Ā—Ź –≤ –°–ł–Ķ–Ĺ–Ķ (–ź—Ą—Ä–ł–ļ–į) –Ņ—Ä—Ź–ľ–ĺ –Ĺ–į–ī –≥–ĺ–Ľ–ĺ–≤–ĺ–Ļ, –≤ –ź–Ľ–Ķ–ļ—Ā–į–Ĺ–ī—Ä–ł–ł, –ļ–ĺ—ā–ĺ—Ä–į—Ź —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–į –ĺ—ā —ć—ā–ĺ–≥–ĺ –ľ–Ķ—Ā—ā–į –Ĺ–į 800 –ļ–ł–Ľ–ĺ–ľ–Ķ—ā—Ä–ĺ–≤, –ĺ–Ĺ–ĺ –ĺ—ā–ļ–Ľ–ĺ–Ĺ—Ź–Ķ—ā—Ā—Ź –ĺ—ā –≤–Ķ—Ä—ā–ł–ļ–į–Ľ–ł –Ĺ–į 7¬į. –≠—Ä–į—ā–ĺ—Ā—Ą–Ķ–Ĺ –∑–į–ļ–Ľ—é—á–ł–Ľ, —á—ā–ĺ –Ķ—Ā–Ľ–ł –ł–∑ —Ü–Ķ–Ĺ—ā—Ä–į –ó–Ķ–ľ–Ľ–ł –°–ĺ–Ľ–Ĺ—Ü–Ķ –≤–ł–ī–Ĺ–ĺ –Ņ–ĺ–ī —É–≥–Ľ–ĺ–ľ 7¬į –ł, —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć –∑–Ķ–ľ–Ĺ–ĺ–≥–ĺ —ą–į—Ä–į —Ä–į–≤–Ĺ–į 360:7¬į—Ö800 = 41 140 –ļ–ł–Ľ–ĺ–ľ–Ķ—ā—Ä–ĺ–≤.
–°–≤—č—ą–Ķ –ī–≤—É—Ö —ā—č—Ā—Ź—á–Ķ–Ľ–Ķ—ā–ł–Ļ –ē–≤–ļ–Ľ–ł–ī, –ī–į–≤—ą–ł–Ļ –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–Ĺ–ĺ —É–ī–į—á–Ĺ–ĺ–Ķ –ł —Ā—ā—Ä–ĺ–Ļ–Ĺ–ĺ–Ķ –ł–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł, –Ī—č–Ľ –Ĺ–Ķ–Ņ—Ä–Ķ—Ä–Ķ–ļ–į–Ķ–ľ—č–ľ –∑–į–ļ–ĺ–Ĺ–ĺ–ī–į—ā–Ķ–Ľ–Ķ–ľ –≤ —ć—ā–ĺ–Ļ –ĺ–Ī–Ľ–į—Ā—ā–ł –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ł. –Ē–į–∂–Ķ –Ĺ–Ķ–ľ–Ķ—Ü–ļ–ł–Ļ —Ą–ł–Ľ–ĺ—Ā–ĺ—Ą –ė–ľ–į–Ĺ–Ĺ—É–ł–Ľ –ö–į–Ĺ—ā —Ā—á–ł—ā–į–Ľ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—é –ē–≤–ļ–Ľ–ł–ī–į –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ–Ļ. –ě–ī–Ĺ–į–ļ–ĺ –Ī—č–Ľ–ł –Ĺ–Ķ—Ź—Ā–Ĺ–ĺ—Ā—ā–ł –≤ –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤–ĺ–ľ –ł–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł–ł –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –Ĺ–Ķ —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź–Ľ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ĺ–≤. –≠—ā–ĺ –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –ļ –ī–į–Ĺ–Ĺ–ĺ–Ļ –Ņ—Ä—Ź–ľ–ĺ–Ļ, –ļ–ĺ—ā–ĺ—Ä—É—é –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–ĺ–≤–Ķ—Ā—ā–ł –≤ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł —á–Ķ—Ä–Ķ–∑ –ī–į–Ĺ–Ĺ—É—é —ā–ĺ—á–ļ—É –ź. –ē–≤–ļ–Ľ–ł–ī —Ā—á–ł—ā–į–Ľ —ć—ā–ĺ –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –į–ļ—Ā–ł–ĺ–ľ–ĺ–Ļ, –į –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–ł –Ņ–ĺ–∑–∂–Ķ –Ņ–ĺ–Ņ—č—ā–į–Ľ–ł—Ā—Ć –ī–ĺ–ļ–į–∑–į—ā—Ć —ć—ā–ĺ—ā —Ą–į–ļ—ā, –ļ–į–ļ —ā–Ķ–ĺ—Ä–Ķ–ľ—É. –ě–ī–Ĺ–į–ļ–ĺ –Ĺ–į –Ņ—Ä–ĺ—ā—Ź–∂–Ķ–Ĺ–ł–ł –≤–Ķ–ļ–ĺ–≤ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤ –Ĺ–ł–ļ—ā–ĺ –Ĺ–Ķ –Ĺ–į—Ö–ĺ–ī–ł–Ľ.
 –Ę–ł—ā—É–Ľ—Ć–Ĺ–į—Ź —Ā—ā—Ä–į–Ĺ–ł—Ü–į –ł–∑ —ā—Ä—É–ī–į –Ě. –ė. –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ĺ–≥–ĺ
–Ę–ł—ā—É–Ľ—Ć–Ĺ–į—Ź —Ā—ā—Ä–į–Ĺ–ł—Ü–į –ł–∑ —ā—Ä—É–ī–į –Ě. –ė. –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ĺ–≥–ĺ–≠—ā—É –∑–į–≥–į–ī–ļ—É –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł —Ä–Ķ—ą–ł–Ľ –Ņ—Ä–ĺ—Ą–Ķ—Ā—Ā–ĺ—Ä –ö–į–∑–į–Ĺ—Ā–ļ–ĺ–≥–ĺ —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –Ě. –ė. –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ł–Ļ, –ĺ–Ņ—É–Ī–Ľ–ł–ļ–ĺ–≤–į–≤—ą–ł–Ļ –ĺ —Ā–≤–ĺ–Ķ–ľ –ĺ—ā–ļ—Ä—č—ā–ł–ł –≤ 1826 –≥–ĺ–ī—É. –Ě–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –Ņ–ĺ–∑–∂–Ķ –ļ –Ņ–ĺ–ī–ĺ–Ī–Ĺ—č–ľ –≤—č–≤–ĺ–ī–į–ľ –Ņ—Ä–ł—ą–Ľ–ł –Ĺ–Ķ–ľ–Ķ—Ü–ļ–ł–Ļ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –ö–į—Ä–Ľ –ď–į—É—Ā—Ā –ł –≤–Ķ–Ĺ–≥–Ķ—Ä—Ā–ļ–ł–Ļ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –Į–Ĺ–ĺ—ą –Ď–ĺ—Ź–ł. –ě–Ī–į —É—á–Ķ–Ĺ—č—Ö —É—Ā—ā–į–Ĺ–ĺ–≤–ł–Ľ–ł, —á—ā–ĺ –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –Ĺ–Ķ–Ľ—Ć–∑—Ź –ī–ĺ–ļ–į–∑–į—ā—Ć –≤ –≤–ł–ī–Ķ —ā–Ķ–ĺ—Ä–Ķ–ľ—č. –ö –Ņ—Ä–ł–ľ–Ķ—Ä—É, –Ķ—Ā–Ľ–ł –ī–ĺ–Ņ—É—Ā—ā–ł—ā—Ć –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –Ņ—Ä–ĺ–≤–Ķ—Ā—ā–ł —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ—É –Ī–ĺ–Ľ–Ķ–Ķ –ĺ–ī–Ĺ–ĺ–Ļ –Ņ—Ä—Ź–ľ–ĺ–Ļ, –Ĺ–Ķ –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—Č–Ķ–Ļ—Ā—Ź —Ā –ī–į–Ĺ–Ĺ–ĺ–Ļ, —ā–ĺ –ľ—č –Ņ—Ä–ł–ī–Ķ–ľ –ļ –ī—Ä—É–≥–ĺ–ľ—É –≤–ł–ī—É –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł - –Ĺ–Ķ–Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤–ĺ–Ļ, –≤ –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ, —ć—ā–ł—Ö –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł–Ļ –Ĺ–į–Ī–Ľ—é–ī–į—ā—Ć—Ā—Ź –Ĺ–Ķ –Ī—É–ī–Ķ—ā. –Ę–į–ļ—É—é –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—é –Ņ–ĺ–∑–∂–Ķ –Ĺ–į–∑–≤–į–Ľ–ł –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ĺ–≥–ĺ.
–í –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ĺ–≥–ĺ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č–Ķ –Ņ—Ä—Ź–ľ—č–Ķ –Ĺ–Ķ –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –ī—Ä—É–≥ —Ā –ī—Ä—É–≥–ĺ–ľ –≤ —Ā–ł–Ľ—É —Ā–į–ľ–ĺ–≥–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł. –ě—Ā–Ĺ–ĺ–≤–Ĺ–ĺ–Ķ –ĺ—ā–Ľ–ł—á–ł–Ķ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ĺ–≥–ĺ –ĺ—ā –Ķ–≤–ļ–Ľ–ł–ī–ĺ–≤–ĺ–Ļ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ, —á—ā–ĺ —á–Ķ—Ä–Ķ–∑ –ĺ–ī–Ĺ—É —ā–ĺ—á–ļ—É, –Ĺ–Ķ –Ľ–Ķ–∂–į—Č—É—é –Ĺ–į –ī–į–Ĺ–Ĺ–ĺ–Ļ –Ņ—Ä—Ź–ľ–ĺ–Ļ, –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–ĺ–≤–Ķ—Ā—ā–ł –Ĺ–Ķ –ĺ–ī–Ĺ—É, –į –Ņ–ĺ –ļ—Ä–į–Ļ–Ĺ–Ķ–Ļ –ľ–Ķ—Ä–Ķ 2 –Ĺ–Ķ –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—Č–ł—Ö –Ķ—Ď –Ņ—Ä—Ź–ľ—č—Ö, –Ĺ–į—Ö–ĺ–ī—Ź—Č–ł—Ö—Ā—Ź –≤ —ā–ĺ–Ļ –∂–Ķ –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā–ł.
–í –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł –õ–ĺ–Ī–į—á–Ķ–≤—Ā–ļ–ĺ–≥–ĺ —Ā—É–ľ–ľ–į –≤—Ā–Ķ—Ö —É–≥–Ľ–ĺ–≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ľ–Ķ–Ĺ—Ć—ą–Ķ 180 –≥—Ä–į–ī—É—Ā–ĺ–≤. –Ē–≤–į –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–į –ł—Ā—Ö–ĺ–ī—Ź—Č–ł–Ķ –ł–∑ –ĺ–ī–Ĺ–ĺ–Ļ –Ņ—Ä—Ź–ľ–ĺ–Ļ –≤—Ā–Ķ –ī–į–Ľ—Ć—ą–Ķ –ł –ī–į–Ľ—Ć—ą–Ķ –Ī—É–ī—É—ā –ĺ—ā—Ö–ĺ–ī–ł—ā—Ć –ī—Ä—É–≥ –ĺ—ā –ī—Ä—É–≥–į.